On the statistical equivalence of restrained-ensemble simulations with the maximum entropy method
By Benoı̂t Roux, and Jonathan Weare.
Published in Journal of Chemical Physics 138(8): 084107 on February 28, 2013. PMID: 23464140. PMCID: PMC3598863. Link to Pubmed page.
Core Facility: Computational Modeling
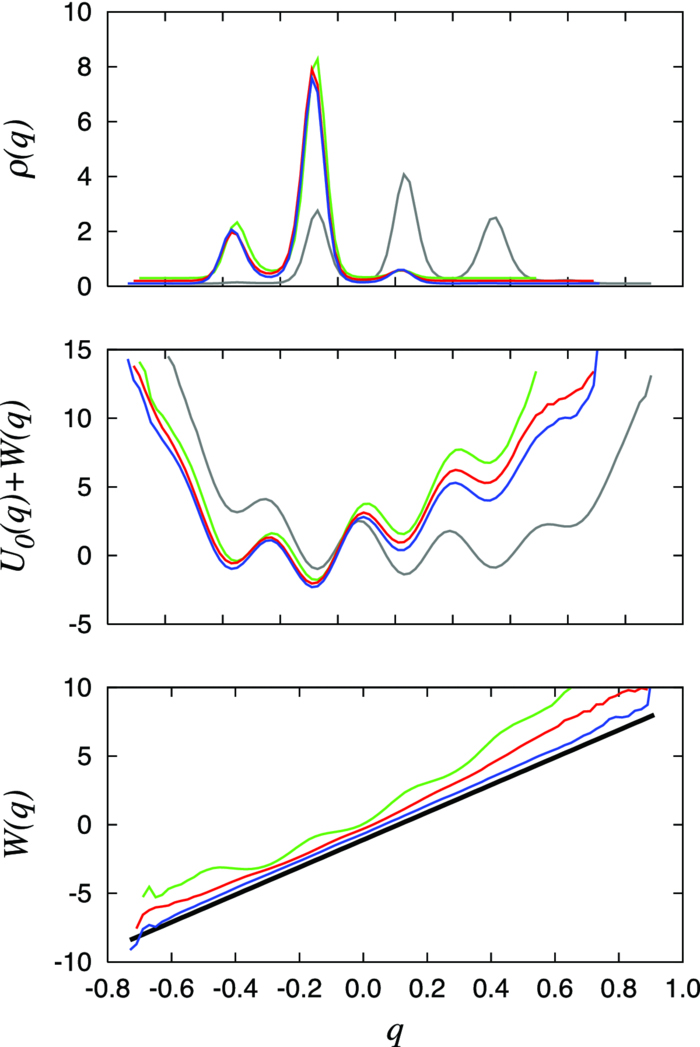
Figure 1. Illustration of the equivalence of the constrained ensemble and the maximum entropy method using the simple 1D model for property q with βU0(q) = 25(q − 0.25)4 − 5.0 − qcos (q) + (1.0/(q2 + 0.5))sin (20q). The unperturbed distribution ρ0(q) (top) and the energy U0(q) (middle) are shown as a gray line. The unperturbed average ⟨q⟩ from the model is 0.258. According to the maximum entropy method, a Lagrange multiplier λ equal to 10.0 is required to shift the average to a value of −0.127. Constrained ensemble with N = 5 (green), 10 (red), and 100 (blue) were simulated using Metropolis Monte Carlo to generate the distribution ρ(q) (top), the effective total potential of mean force [U0(q) + W(q)] (middle), and the mean effect of the ensemble on one single replica W(q) (bottom). The net effect of the constrained ensemble is to produce a linear shift λq, with λ = 10, which is equivalent to that from the maximum entropy method (black line). The ensemble average (q1 + … + qn)/N = Q was strictly imposed via a delta function in the Monte Carlo simulations. All the curves were offset very slightly for better visualization.
Abstract
An issue of general interest in computer simulations is to incorporate information from experiments into a structural model. An important caveat in pursuing this goal is to avoid corrupting the resulting model with spurious and arbitrary biases. While the problem of biasing thermodynamic ensembles can be formulated rigorously using the maximum entropy method introduced by Jaynes, the approach can be cumbersome in practical applications with the need to determine multiple unknown coefficients iteratively. A popular alternative strategy to incorporate the information from experiments is to rely on restrained-ensemble molecular dynamics simulations. However, the fundamental validity of this computational strategy remains in question. Here, it is demonstrated that the statistical distribution produced by restrained-ensemble simulations is formally consistent with the maximum entropy method of Jaynes. This clarifies the underlying conditions under which restrained-ensemble simulations will yield results that are consistent with the maximum entropy method.
Note: This article was identified by the Journal of Chemical Physics as being on the list of Top 20 Most Read of March 2013.


